Single-Level Uncapacitated Lotsizing Problem
This problem is also known as the Wagner-Whitin problem.
Assumptions:
- |
a single item is considered |
- |
demands are dynamic (period-specific, days, weeks, etc.) |
- |
the capacity of the resource is neglected |
There are several mathematical formulations for this problem. The most common model reads as follows:
$\mathrm{Minimize Z}=\displaystyle{\sum_{t=1}^T \big( {h\cdot y_t}+{ s\cdot \gamma _t} \big)}
subject to:
$y_{t-1}+q_t-y_t=d_t \qquad {t=1,2,\ldots,T}$
$q_t-M\cdot \gamma _t\le 0 \qquad {t=1,2,\ldots,T}$
$q_t\geq 0 \qquad {t=1,2,\ldots,T}$
$y_t\geq 0 \qquad {t=1,2,\ldots,T}$
$\gamma _t\in \left\{ {0,\,1} \right\} \qquad {t=1,2,\ldots,T}$
Symbols:
| $d_t$ | demand in period $t$ |
| $h$ | holding costs |
| $M$ | big number (M must be greater than the maximum lot size) |
| $s$ | setup costs |
| $T$ | length of the planning horizon |
| $q_t$ | lot size in period $t$ |
| $y_t$ | inventory at the end of period $t$ |
| $\gamma_t$ | binäry setup variable |
Every optimum solution to this model satifies the so-called ZIO (zero-inventory-ordering) condition. This means that in any period $t$ either the beginning inventory $y_{t-1}$ or the lot size $q_t$ are zero, i.e. $y_{t-1}\cdot q_t=0$. This property allows to reformulate the above model as a shortest-route model.
Example: Consider a product with the following demands: $d_1=20$, $d_2=80$, $d_3=160$, $d_4=85$, $d_5=120$ and $d_6=100$. The setup costs are $s=500$ and the holding costs are $h=1$.
The corresponding shortest-route network is:
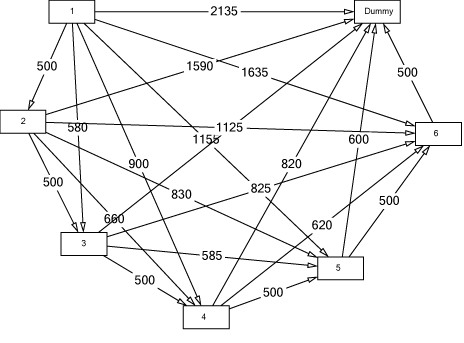
For each period there is a node. An arrow starting at node $i$ and ending at node $j$ means: the lot produced in period $i$ covers the demand from period $i$ to period $j-1$. The numbers associated to the arrows are the setup and holding costs that result from the corresponding lot size.
Using any appropriate shortest-route algorithm (e.g. Dijkstra'a algorithm), we get the following solution:
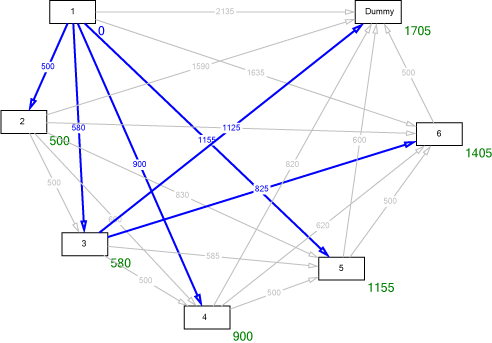
Going backwards from node "Dummy" to node "1" we find, that the optimum predecessor of "Dummy" is "3" (production quantity in period 3: $q_3=465$). Next, the optimum predecessor of "3" is "1" (production quantity in period 1: $q_1=100$). The total costs are 1705.
In industrial practice, heuristic solution procedures are used, such as
- Silver-Meal heuristic
- Least unit-cost heuristic
- Part-period heuristic
- Groff heuristic
and many others.
» See also: MLCLSP - Multi-level capacitated dynamic lotsizing problem